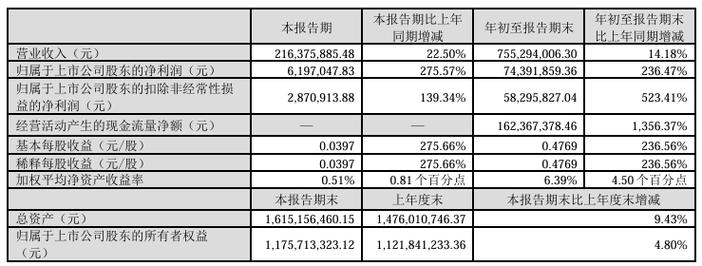
一家家政做事公司,假设师傅每天事情 8 个小时,假定一天 n 个订单,每个订单其占用韶光长为 Ti,挣取代价为 Vi,现请你为师傅安排订单,并担保师傅挣取代价最大。
输入格式输入 n 组数据,每组以逗号分隔,并且每一个订单的编号、时长、挣取代价以空格分隔输出格式输出争取代价和订单编号,订单编号按照代价由大到小排序,争取代价相同,则按照每小时均匀争取代价由大到小排序

示例:输入:[MV10001 2 100,MV10008 2 30,MV10003 1 200,MV10009 6 500,MV10010 3 400]输出:730 MV10010 MV10003 MV10001 MV10008输入:[M10001 2 100,M10002 3 210,M10003 3 300,M10004 2 150,M10005 1 70,M10006 2 220,M10007 1 10,M10008 3 30,M10009 3 200,M10010 2 400]输出:990 M10010 M10003 M10006 M10005

由于本题每个订单每天只被安排一次,是范例地采取 动态方案 求解的 01 背包问题。
动态方案观点动态方案过程:每次决策依赖于当前状态,又随即引起状态的转移。一个决策序列便是在变革的状态中产生出来的,以是,这种多阶段最优化决策办理问题的过程就称为动态方案。
动态方案事理:动态方案与分治法类似,都是把原问题拆分身分歧规模相同特色的小问题,通过探求特定的递推关系,先办理一个个小问题,终极达到办理原问题的效果。
建立动态方程假设,师傅挣取代价最大时的订单为 x1,x2,x3,...,xi(个中 xi 取 1 或 0,表示第 i 个订单被安排或者不安排),vi 表示第 i 个订单的代价,wi 表示第 i 个订单的耗时时长,wv(x, j) 表示安排了第 i 个订单,师傅总耗时为 j 时的最大代价。
可得订单代价和耗时的关系图:
i
1
2
3
4
5
w(i)
2
2
1
6
3
v(i)
100
30
200
500
400
因此,可得 动态方程:
解释:j < w(i) 表示订单不被安排,j ≥ w(i) 表示订单被安排。
确定边界可以确定边界条件 wv(0, j) = wv(i, 0) = 0,wv(0, j) 表示一个订单都没安排,再怎么耗时价值都为 0,wv(i, 0) 表示没有耗时,安排多少订单代价都为 0。
求解
求解过程,可以填表来进行仿照:
1. 如 i=1,j=1 时,有 j < w(i),故 wv(1, 1) = wv(1-1, 1) = 0;
2. 又如 i=1,j=2 时,有 j = w(i),故 wv(1, 2) = max(wv(1-1, 1), wv(1-1, 2-w(1)) + v(1) = 100;
3. 如此下去,直至填到末了一个,i=5,j=8 时,有 j < w(i),故 wv(5, 8) = max(wv(5-1, 8), wv(5-1, 8-w(5)) + v(5) = 730;
4. 在耗时没有超过 8 小时的条件下,当前 5 个订单都被安排过期,wv(5, 8) = 730 即为所求的最大代价;
解的组成
只管 求解 过程已经求出了最大代价,但是并没有得出哪些订单被安排了,也便是没有得出解的组成部分。
但是在求解的过程中不难创造,寻解方程知足如下定义:
从表格右下到左上为寻解方向,寻解过程如下:
i=5,j=8 时,有 wv(5, 8) != wv(4, 8),故 x(5) = 1,此时 j -= w(5),j = 5;i=4 时,无论 j 取何值,都有 wv(4, j) == wv(3, j),故 w(5) = 0,此时 j = 5;i=3,j=5 时,有 wv(3, 5) != wv(2, 5),故 x(3) = 1,j -= w(3),j = 4;i=2,j=4时,有 wv(2, 4) != wv(1, 4),故 x(2) = 1,j -= w(2),j = 2;i=1,j=2时,有 wv(1, 2) != wv(0, 2),故 x(1) = 1,j -= w(1),j = 0; 寻解结束;
编码实现实现的代码如下,并将逐一详细解释。
class Knapsack{ //物品重量,index从1开始表示第1个物品 public $w = array(); //物品代价,index从1开始表示第1个物品 public $v = array(); //最大代价,$wv[$i][$w]表示前i个物品重量为w时的最大代价 public $wv = array(); //物品总数 public $n = 0; //物品总重量 public $W = 0; //背包中的物品 public $goods = array(); / Knapsack constructor. @param array $goods 物品信息,格式如下: [ [index, w, v] //good1 ... ] @param $c / public function __construct(array $goods, $c) { $this->goods = $goods; $this->W = $c; $this->n = count($goods); //初始化物品代价 $v = array_column($goods, 2); array_unshift($v, 0); $this->v = $v; //初始化物品重量 $w = array_column($goods, 1); array_unshift($w, 0); $this->w = $w; //初始化最大代价 $this->wv = array_fill(0, $this->n + 1, array_fill(0, $this->W + 1, 0)); $this->pd(); $this->canPut(); } public function getMaxPrice() { return $this->wv[$this->n][$this->W]; }}
动态求解过程:
public function pd(){ for ($i = 0; $i <= $this->W; $i++) { for ($j = 0; $j <= $this->n; $j++) { //未放入物品和重量为空时,代价为0 if ($i == 0 || $j == 0) { continue; } //决策 if ($i < $this->w[$j]) { $this->wv[$j][$i] = $this->wv[$j - 1][$i]; } else { $this->wv[$j][$i] = max($this->wv[$j - 1][$i], $this->wv[$j - 1][$i - $this->w[$j]] + $this->v[$j]); } } }}
寻解过程:
public function canPut(){ $c = $this->W; for ($i = $this->n; $i > 0; $i--) { //背包质量为c时,前i-1个和前i-1个物品代价不变,表示第1个物品未放入 if ($this->wv[$i][$c] == $this->wv[$i - 1][$c]) { $this->goods[$i - 1][3] = 0; } else { $this->goods[$i - 1][3] = 1; $c = $c - $this->w[$i]; } }}
按照订单代价降序获取订单信息(若订单代价相同则按单位韶光均匀代价降序排列):
public function getGoods(){ $filter = function($value) { return $value[3]; }; $goods = array_filter($this->goods, $filter); usort($goods, function($a, $b) { if ($a[2] == $b[2]) { if ($a[2] / $a[1] < $b[2] / $b[1]) { return 1; } return 0; } return $a[2] < $b[2]; }); return $goods;}
吸收标准输入处理并输出结果:
$arr = explode(',', $input);$filter = function ($value) { return explode(' ', $value);};$knapsack = new Knapsack(array_map($filter, $arr), 8);$goods = $knapsack->getGoods();echo $knapsack->getMaxPrice(), ' ', implode(' ', array_column($goods, 0)), PHP_EOL;总结
该题利用动态方案求解,算法的韶光繁芜度为 O(nc),当然也可以采取其他办法求解。例如先将订单按照代价排序,然后依次考试测验进行安排订单,直至剩余耗时不能再被安排订单。
有关动态方案的其他范例运用,请参考 常见的动态方案问题剖析与求解 一文。