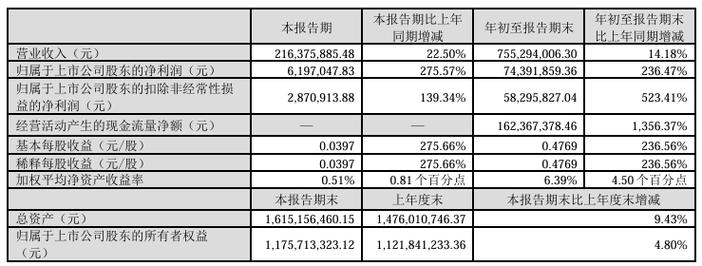
在计算机科学中,子集合是一个基础且重要的概念。它涉及到集合论、算法设计、数据结构等多个领域。本文将从子集合的定义、性质、应用以及价值等方面进行阐述,以期为读者提供全面、深入的见解。
一、子集合的定义及性质

1. 定义
子集合是指一个集合A的所有元素的集合,称为A的子集。用数学符号表示为:B?A。如果B是A的子集,那么B中的任意元素都属于A。
2. 性质
(1)空集是任何集合的子集。即??A。
(2)任何集合都是自身的子集。即A?A。
(3)子集的子集仍然是子集。即如果B?A,那么B的任意子集也是A的子集。
(4)集合A和它的子集之间具有包含关系。即B?A或A?B。
二、子集合在计算机科学中的应用
1. 数据结构
在数据结构中,子集合的概念广泛应用于各种数据结构,如数组、链表、树等。通过子集合,可以实现数据的分割、合并、查找等操作。
2. 算法设计
子集合在算法设计中发挥着重要作用。例如,在二分查找、快速排序等算法中,子集合用于缩小搜索范围,提高算法效率。
3. 图论
在图论中,子集合可用于表示节点、边等元素。通过子集合,可以研究图的性质、路径、连通性等问题。
4. 集合运算
集合运算包括并集、交集、差集等。子集合是这些运算的基础,例如,集合A和集合B的交集可以表示为A的子集。
5. 程序设计
在程序设计中,子集合可用于表示数组、列表等数据结构。通过子集合,可以方便地实现数据的处理和操作。
三、子集合的价值
1. 提高算法效率
通过子集合,可以缩小搜索范围,提高算法效率。例如,在二分查找中,子集合的使用使得算法的时间复杂度降低为O(logn)。
2. 便于数据管理
子集合可以方便地实现数据的分割、合并、查找等操作,从而提高数据管理的效率。
3. 促进计算机科学的发展
子集合在计算机科学中的应用广泛,为计算机科学的发展提供了有力支持。
子集合是计算机科学中的一个基础且重要的概念。通过对子集合的定义、性质、应用以及价值的阐述,本文旨在为读者提供全面、深入的见解。在今后的学习和研究中,我们应充分认识子集合的重要性,充分发挥其在计算机科学中的应用价值。