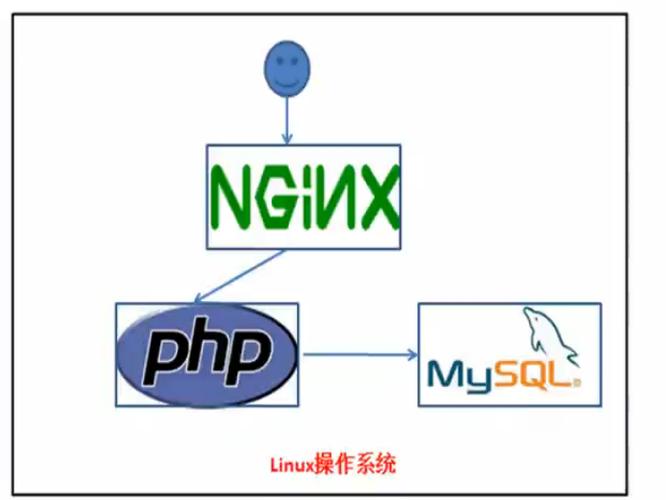
例题之后紧随着的做一做部分中有一道题目:1+3+5+……+15+17+19=多少?这是前10项奇数的求和。同时练习题第5题有一题打算2+4+6+……+16+18+20,这是前10项偶数的求和,涉及的都是公差为2的数列,1个到19,1个到20整体打算难度不大。
本日看了两套试题,创造这种等差数列求和不断被用到,第一个题目奇数从一加到了39。第二个题目成了偶数从2加到98。然后,数线段、数角少的时候是要挨个数的(一样平常也是哀求挨个数),但逐渐到高年级可能便是打算,尤其是碰到给定20个点(边),30个点(边)时,挨个数都可能数不清。

关于等差数列的通项公式或求和公式算法如果小学老师都教了,那家长当然可以用求和公式来求和,乃至是用通项公式确定项数。

但如果没有教,那么还是要按小学例题给的思路,头加尾然后数多少项,但详细的项数确定还真随意马虎出错,比如从2加到79,老师是否有教总项数的打算呢?奇数个项的和与偶数个项的和中间项该如何去找?
当然高中阶段基本上就很少涌现这种公差为1或2的整数和了,正负数的公差不断涌现,乃至分数也常常涌现。但高中阶段稽核的便是公式的运用。
在高中阶段公式的推导是正反相加,还是有别于小学阶段的教法的,也看过一本小学数列求和的方法,由于公差有正负之分,但在四年级学生并没有打仗过负数,以是编者在写通项公式时隐去了公差的定义,公差为负定义为是递减数列,以是会看到an=a1-(n-1)d这种形式,求和公式推导和高中同等。一起看下,例题是奥林匹克题目,不妨也试一试。
现在只想知道,前n项和的公式是否须要节制。