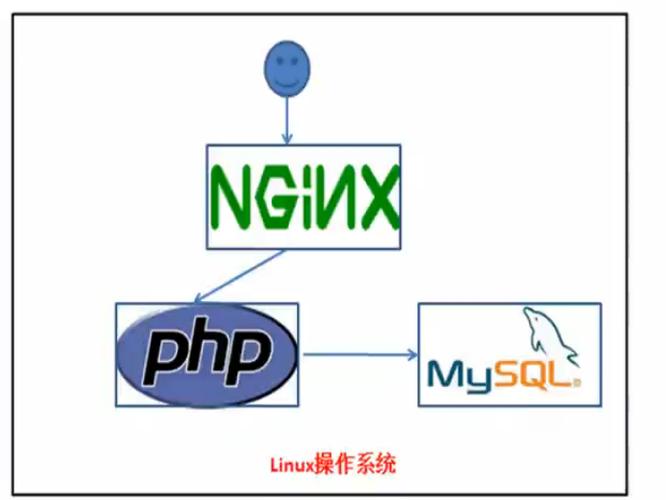
“李白打酒”是我国民间自古以来广为流传的一道打以油诗的形式表述的运用题,这首打油诗讲的便是现在小学数学必考运用题之一——还原问题。
还原问题顾名思义,便是已知结果,一步步逆推,逐步靠拢条件,终极将问题办理。

比如在小学数学运用题中,常常会碰到这样一类题:在某一次运算或列式中某人由于马虎而抄错数字或者符号,得出错误的结果,末了要打算精确的结果是多少:

方块猴把一个加数个位上的9算作6,十位上的6算作了9,得到了缺点的结果130,那么机警的小朋友知道精确的和该当是多少吗?
很多孩子面对这种类型的题目,大脑一片空缺,无从下手。
一顿操作猛如虎,填上一个数字,答案还可能是缺点的。
解答这类问题的要点在于“还原”,即从末了一个已知数出发,逐步逆推回去,也便是古语中常说的“反其道而行之”。剖析每一步变革和未知数的关系,结合四则运算法则,利用逆运算逐步推导出精确结果。
看起来很繁芜,火花L5《还原剖析》专题总结了朗朗上口的还原问题童谣,帮助孩子捋清思路:
加法要变减,减法要变加
乘法变除法,除法能变乘
用好这个口诀,文章开头提到的题目,轻轻松松就能做出来了。
个位的9→6,实在是将精确结果减少3,十位的6→9,实在是将精确结果增加了30。
再画一画顺序图,将加法变减法,减法变加法,精确结果就能倒推出来了,答案为103。
图片来源于火花课件
p.s.小火花以为在刚打仗这类运算时,画出顺序图是特殊好的一个做法,避免列算式表达时,碰着须要"先算加减法,后算乘除法"时会忘却写括号的问题。
上面提到的根据“缺点结果结合四则运算一步步倒推精确结果"只是一种解法,还可以利用“倒推另一个加数法”结合四则运算求出精确的结果,这个在火花L5课程当中有详细的先容~小朋友们听课的时候可以比拟一下这两种方法,解题的时候找到最适宜的一种。
“还原问题”和较繁芜的笔墨表述结合在一起,难度就升级了。
三角兔有一本新的故事书,第一天看了这本书的一半又3页,第二天看了余下的一半少3页,第三天又看了8页,剩下5页,这本故事书一共有多少页?
绕圈圈绕得都快糊涂啦,一下子“一半又3”,一下子“一半少3”,可以用算式和孩子阐明:
一半又3:新书页数÷2+3
一半少3:第一次余下的页数÷2-3
将笔墨表述转化成算式表达,题意一明朗,再用倒推法立时就能得出答案。
图片来源于火花课件
“一半型”、“倍数型”不仅将倒推法和运用题完美结合,还能够帮助孩子理解常见的数学措辞如“一半又”、“一半少”、“一半多”、“增加(减少)一倍”等含义,提升数学阅读理解能力。
上面提到的几种题型,都属于单项变量还原问题,双向乃至多项变量还原问题是也是小学数学常考形式:
一共有34枚金币,从左边分一半金币到右边,再从右边分一半金币到左边,现在左边比右边多6枚金币,那一开始两边各有多少枚?
多变量还原问题只要捉住“给来给去和不变”这条定律,不管是几个数之间经由多少组运算,都能做到一挥而就。
图片来源于火花课件
除了还原问题,火花L4课程《加减数学迷》、《路线方案游戏进阶》等课程中也涉及到了逆向思维的培养。
在日后数学学习的过程中,会创造有很多问题如果顺着题目的思路去思考,会走不少弯路,但是如果改变思考的顺序,从结果出发,反其道而行之,解起题来就大略的多。
好了,说了这么多,文章开头“李白打酒”的问题,你有答案了吗?在留言区写出你的答案吧!